Sprouts

Players: 2 
Ages: 5 and up
Cost: Free!
Math Ideas: logical deduction, spatial reasoning
Questions to Ask: 
   "How many connections does each point have?"
   "How many moves do you think this game will last?
   "What if we played with only one starting dot? Who would win?"

I have officially entered the long, dark period of parenting known as The Age of After-School Activities.

As I write this newsletter, I am sitting in a restaurant, having eaten a dinner I didn't need just to justify leeching off their Wifi for an hour while my son is at Torah Time.

Fortunately, in the previous hour I got to pick him up from school, take him to get some frozen yogurt, and play a quick few rounds of a new game that I'm really enjoying: Sprouts.

How to Play

Sprouts is a free 2-player game that you can play with pencil and paper.

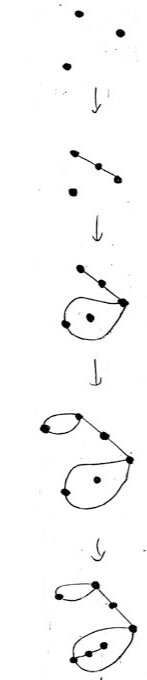
Start by placing a few points randomly around a page. I'd recommend three points to start.

Each player takes turns drawing a line, or curve, to connect one point to another (or back to itself). Then, somewhere along that line, you place a new point, which breaks the line you drew into two smaller segments.

The next player then draws a new line to connect two dots and placing a new dot somewhere along their line. A couple of important rules:

• Once a dot has three connections, it is done. You cannot connect a fourth line segment to that point.

• Lines can curve anywhere you want, but they can never cross each other.

• Lines can also loop back and connect a dot to itself, and this counts as two connections

That's it! If you cannot draw a new line, you lose.

Where's the Math?

I loved introducing this game to my son because it sums up the ways that a conceptually rich game can be meaningful to people of all different levels of mathematical knowledge.

I was obsessed with trying to figure out the underlying structure of the game. Can the game go on forever, in theory? Or will it necessarily end at some point? If it must end, then what is the maximum number of moves in a game with 3 starting points? 4 points? n points?

I was being, in other words, a total nerd about it. (I'll leave those nerdy questions for my fellow nerds to ponder over!)

My son, on the other hand, was being a coldblooded killer. He kept drawing these long, looping lines that just got so complicated and maze-like that I really struggled to find avenues to connect the points! He even started one game by placing all four starting points in the very corners of the paper, which seems to be against the spirit of the game if you ask me and no I'm not bitter that he won that game stop asking me about it.

Seriously, though, I didn't mind, since he was using his spatial reasoning skills to make the game more challenging for me, and consequently for himself! Although technically a squiggle and a straight line have the same effect on the game (the math term is "isomorphic") in practice, the squiggle is waaaaay harder to wrap your head around. So by being deliberately annoying, my son figured out how to confuse me just enough to win. 

I have no idea where he gets it.

Questions to Ask

A good question to ask when introducing the game is "How many connections does each point have?" Your child might need soe practice counting the connections to each point. In the example at left, Point A has three connections, while points D and E each have two connections. Point B has a single connection, while Point C has no connections yet.

Next, you could ask your child "How many moves do you think this game will last?"There is definitely a range of game lengths, depending on player decisions, but there is a clear relationship between the number of starting dots and the number of possible moves in a game. This question might get your child thinking about that relationship.

A final, sort of silly question, is "What if we started with only one dot? How many moves would the game last? Who would win?"

Playing a very simplified version of the game might seem odd at first, but it actually could help your child notice some of the strategy within the larger game. The patterns and structure they encounter with the simple version can lead to great ideas about the more complex game. Mathematicians do this all the time, reducing a problem to its simplest form, then seeing if we can extend our ideas out to the more complex situation. 

I'm not saying your child has to mathematically solve this game! But playing around with the simpler versions might clue them into some insights that they otherwise might miss.